DOĞRUSAL DENKLEM SİSTEMLERİ VE MATRİSLER
2x + 4y = 8
12x + 12y = 36
denklemlerinin ortak çözümü nedir?
Birinci denklemden y’yi çekelim isterseniz.
y = (8 − 2x)/4 = 2 − 1/2x olur. Simdi de bunu diğer denklemde yerine yazalım.
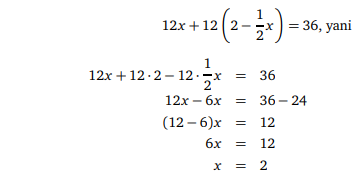
y = 2 − 1/2x bulmuştuk, şimdi bu denklemde bulduğumuz x degerini yani 2’yi yerine yazalım.
y = 2 − 1/2 · 2 = 2 − 1 = 1
4x + 3y = 18
6x − 3y = 12
Denklemlerinin çözümü nedir?
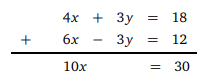
3y ile −3y sadeleşti ve x = 30/10 = 3 çıktı. Bir denklemde yerine yazalım.
4 · 3 + 3y = 18, 12 + 3y = 18, 3y = 6, y = 2 çıktı. O halde sistemin çözümü (3, 2) noktası oldu.
2x − 3y = −7
x + 6y = 34
Doğrusal denklem sisteminin çözümü nedir?
Önce x ya da y değerlerinin kat sayılarını eşitliyoruz ve ardından taraf tarafa topluyoruz..
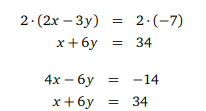
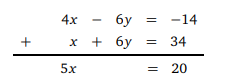
x=4 olur. x = 4 değerini ben ikinci denklemde yerine yazarak y = 5 bulabiliriz. O halde denklem sisteminin çözümü (x, y)=(4, 5) olur.
İki bilinmeyenli her denklem sisteminin her zaman bir çözümü var mıdır? Varsa hep tek midir?
Bu sorunun cevabı olumsuz. Sistemdeki her bir denklem düzlemde bir doğruya karşılık geldiğinden, bu soru geometrik olarak iki doğru her zaman kesişir mi, kesişirse tek noktada mı kesişir sorusuna dönüşür.
Hangi koşullarda doğrular birbirlerine paraleldir?
l1 : y = m1 x + n1
l2 : y = m2 x + n2
olmak üzere m1 = m2 ve n1 ile n2 birbirlerine eşit değil ise doğrular paraleldir.
Hangi durumlarda doğrular çakışık olur?
l1 : y = m1 x + n1
l2 : y = m2 x + n2
olmak üzere m1 = m2 ve n1 = n2 olduğunda doğrular çakışık olur.
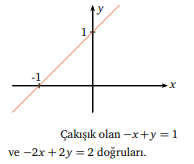
−x + y = 1
−2x + 2y = 2 denklem sistemini oluşturan doğruların grafikleri nasıl olur?
Ikişer ikişer birbirine dıştan teğet olan ve merkezleri A, B ve C olan üç tane çember ve bu çemberlerin merkezlerinin arasındaki uzaklıklar |AB| = 16 birim (br), |AC| = 18 br ve |BC| = 10 br olarak verilirse her bir çemberin yarıçapı nedir?
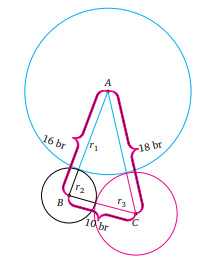
r1 + r2 = 16
r1 + r3 = 18
r2 + r3 = 10
(16 − r1)+(18 − r1) = 10 34 − 2r1 = 10, 2r1 = 24, yani r1 = 12 bulunur.
r2 = 16 − r1 olduğundan r2 = 4
r3 = 18 − r1 olduğundan r3 = 6
x − 2y + 3z = 9
−x + 3y = −4
2x − 5y + 5z = 17
Sisteminin çözümü nedir?


Yeni elde edilen sistemin son iki denklemini toplayıp üçüncü denklemin yerine yazalım:
x − 2y + 3z = 9
y + 3z = 5
2z = 4.
Üçüncü denklem bize doğrudan z bilinmeyeninin değerini verir, 2z = 4’ten z = 2 olur. Bunu ikinci denklemde yerine yazarsak y + 3 · 2 = 5’ten y = −1 olur. Son olarak da birinci denklemde z yerine 2 ve y yerine −1 yazılırsa x −2·(−1)+3·2 = 9’dan x = 1 bulunur. Demek ki çözümümüz x = 1, y = −1 ve z = 2’dir
Hangi durumlarda sistemin çözümü değişmez?
Bir denklem sistemini çözmek için sırasıyla aşağıdaki işlemler uygulanırsa sistemin çözümü değismez.
1. İki denklemin yeri değiştirilebilir,
2. Sistemdeki bir denklem sıfırdan farklı bir sayı ile çarpılabilir,
3. Bir denklem bir sayı ile çarpılıp, sistemdeki diğer bir denkleme eklenebilir.
3x + 5y + 7z=10
2x + 4y − z=6
2x + 4y − z=7
Denklem sisteminin çözümü nedir?
İki denklemin sol yanları eşit fakat sağ yandaki sayılar farklı. Aynı ifade farklı iki sayıya eşit olamayacağı için sistemin hiçbir çözümü yoktur.
Bir matrisin düz yatay ve dikey sırasına ne ad verilir?
Bir matristeki düz yatay bir sıraya matrisin bir satırı, dikey bir sıraya matrisin bir sütunu adı verilir.
Sadece bir satır ya da bir sütundan oluşan matrislere ne ad verilir?
Sadece bir satırdan olu¸san matrise satır matrisi, sadece bir sütundan oluşan matrise sütun matrisi adı verilir.
Matrislerde hangi üç işlem yapılabilir?
Bu işlemler: iki satırın yerlerinin değiştirilmesi; bir satırın sıfırdan farklı bir sayı ile çarpılması; bir satırın bir sayı ile çarpılıp bu çarpımın başka bir satırla toplanmasıdır.
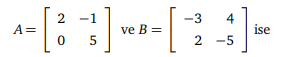 A+B kaçtır?
A+B kaçtır?
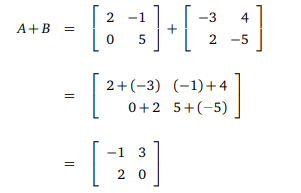
Bir matrisin bütün elemanlarının sıfır olması neyi ifade eder?
Bir matrisin bütün elemanları sıfır ise bu matrise bir sıfır matris denir. Örnegin,
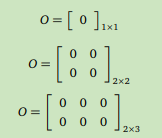
farklı boyutlarda sıfır matrislerdir.
a11 x + a12 y = b1
a21 x + a22 y = b2
doğrusal denklem sistemini matris çarpımı kullanarak nasıl yazabiliriz?
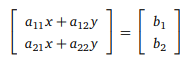
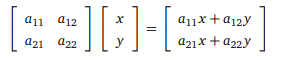
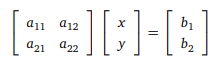
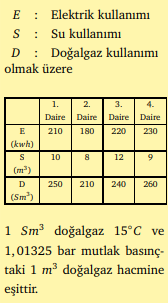
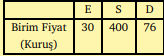
Bir apartmanın her dairesinin harcadığı elektrik, su, doğalgaz miktarları ve bunların birim fiyatları bilinirse her bir dairenin elektrik, su ve doğalgaz giderlerinin toplamını tablolardaki bilgileri kullanarak hesaplayınız.
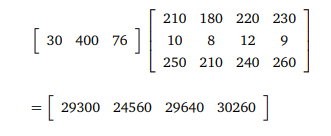
1. Daire için giderler toplamı 29300 kuruş yani 293 TL
2. Daire için giderler toplamı 24560 kuruş yani 245, 60 TL
3. Daire için giderler toplamı 29640 kuruş yani 296, 40 TL
4. Daire için giderler toplamı 30260 kuruş yani 302, 60 TL’dir.
Kare matris nedir?
Satır ve sütun sayıları eşit olan bir matrise bir kare matris denir.
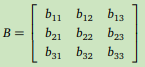 Böyle bir matrise ne ad verilir?
Böyle bir matrise ne ad verilir?
B matrisi 3 × 3 boyutunda bir kare matristir.